Many of the “Getting started” guides for USACO are geared for experienced programmers who can solve the introductory level problems easily. In fact, the official USACO training gateway says, “The techniques taught and drilled here are difficult.”

The following guide is for those who know just enough programming to start attempting bronze level problems; those who are familiar with arrays, nested loops and conditionals in any language, and ready to dive into competitive programming challenges at the bronze level of USACO.

It’s important to follow the steps for solving a programming problem in order, completing each one fully and resisting the temptation to jump ahead. The steps are:

  • Read the problem’s description
  • Examine the input data format and test cases
  • Identify an algorithm to solve the problem
  • Code
    • Read in the input data
    • Implement the algorithm
    • Test the program

We will use the Square Pasture problem from a past USACO contest. You can read it at the source and it is included below for easy reference as we go through the steps to solve it. Even if you find the problem to be easy, follow the steps listed as the goal is to learn how to apply these steps to much harder problems.

Farmer John has decided to update his farm to simplify its geometry. Previously, his cows grazed in two rectangular fenced-in pastures. Farmer John would like to replace these with a single square fenced-in pasture of minimum size that still covers all the regions of his farm that were previously enclosed by the former two fences.

Please help Farmer John figure out the minimum area he needs to make his new square pasture so that if he places it appropriately, it can still cover all the area formerly covered by the two older rectangular pastures. The square pasture should have its sides parallel to the x and y axes.

INPUT FORMAT (file square.in):

The first line in the input file specifies one of the original rectangular pastures with four space-separated integers x1 y1 x2 y2,
each in the range 0…10. The lower-left corner of the pasture is at the point (x1,y1), and the upper-right corner is at the point (x2,y2), where x2>x1 and y2>y1.
The second line of input has the same 4-integer format as the first line, and specifies the second original rectangular pasture. This pasture will not overlap or touch the first pasture.

OUTPUT FORMAT (file square.out):
The output should consist of one line containing the minimum area required of a square pasture that would cover all the regions originally enclosed by the two rectangular pastures.

SAMPLE INPUT:
6 6 8 8
1 8 4 9

SAMPLE OUTPUT:

49

In the example above, the first original rectangle has corners (6,6)
and (8,8). The second has corners at (1,8) and (4,9). By drawing a square fence of side length 7 with corners (1,6) and (8,13), the original areas can still be enclosed; moreover, this is the best possible, since it is impossible to enclose the original areas with a square of side length only 6. Note that there are several different possible valid placements for the square of side length 7, as it could have been shifted vertically a bit.

Read the problem’s description

This step can seem obvious but you need to do it efficiently and effectively. Read the Square Pastures problem description one time from start to finish. It is fine if some parts don’t make sense yet – continue to read the entire description. Then, read it one more time. This time, start to tune out the parts that are unnecessary details and transform the description into mathematical statement-question combinations. Follow along below to see which parts are unnecessary details, and how the verbose description is turned into simpler mathematical statement-questions.

“Farmer John has decided to update his farm to simplify its geometry” – unnecessary detail.

“Previously, his cows grazed in two rectangular fenced-in pastures” – The problem has two rectangles.

“Farmer John would like to replace these with a single fenced-in pasture of minimum size that still covers all the regions of his farm that were previously enclosed by the former two fences.”

We need a square that will entirely cover the two rectangles.

“Please help Farmer John figure out the minimum area he needs to make his new square pasture so that if he places it appropriately, it can still cover all the area formerly covered by the two older rectangular pastures. The square pasture should have its sides parallel to the x and y axes.”
Find the smallest square, parallel to the x and y axes, that will cover both the rectangles.

With practice, you will get good at removing the parts not needed, and transforming the problem into definite mathematical statements and the question to solve.

Examine the input data format and test cases

Any problem will have input data that will test the program. The description of the input data can seem confusing at first. The problem’s authors have to be detailed as they are not available to answer any questions you have.

“The first line in the input specifies one of the original rectangular pastures with four space-separated integers x1 y1 x2 y2, each in the range 0..10. The lower-left corner of the pasture is at the point (x1,y1) and the upper-right corner is at the point (x2,y2) where x2 > x1 and y2 >y1.”

This seems like a lot to take in, but the above lines are simply giving the lower-left and top-right coordinates of a rectangle. Now is a good time to grab a pencil and paper.

“The second line of input has the same 4-integer format as the first line, and specifies the second original rectangular pasture. This pasture will not overlap or touch the first pasture.”

Do not rush through the above lines. They contain a key detail: the rectangles do not overlap or touch. Draw the two rectangles on paper. Draw one side of the square that can cover both the rectangles. Next, read the explanation of the sample test case’s output.

Along with examining the input test cases, note how the output needs to be printed. In this case, the output should be on a separate line and it should be the area of the final square. They are not asking for the coordinates of the square or its side.

Identify an algorithm to solve the problem

At this point, you will be raring to go and want to start coding with the ideas forming in your mind. Don’t. Take the time to properly identify your algorithm or you will end up redoing most parts of your code. Draw more rectangle pairs on the paper, and find the square that covers each pair of rectangles.

For each pair of rectangles, note down the x1, y1, x2, y2 coordinates and the side of each square that completely covers them. As you create more such test cases, you will start to notice a pattern. Look closely at the figures and try to find a relationship between the coordinates and the side of the final square. In the image below, the side of the square is drawn in three examples. What would be the length of the square’s side in the fourth example?

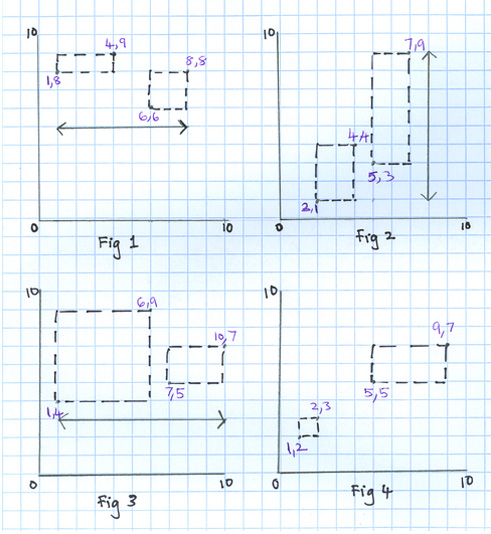
As you can see, the square’s side extends from the smallest x coordinate to the biggest. Or from the smallest y coordinate to the biggest. So, you would need to find the biggest and smallest x coordinates (call them maxX and minX). And, find the biggest and smallest y coordinates (call them maxY and minY).

The side of the square to cover both the rectangles would be whichever of the two below is greater:
abs(maxY – minY)      abs(maxX – minX)

Code

Read the input data
The input data is usually one or more lines of numbers or strings separated by spaces. Based on your algorithm, you will decide how you will store the input data. In most beginner problems, you will use a 1D or 2D array (list) to store the input data. While you are still new to competitive programming, always do this – print the input data to check that the program has read it in correctly. A common mistake is to store numbers as strings instead of integers.Printing and checking the data will ensure that mistakes like this do not happen.

In the Square Pastures problem, you may want to store the 4 x coordinates in one array  and the 4 y coordinates in another array. This will make it easier to find the smallest and biggest x and y coordinates.

Implement the algorithm
Now, time for the real action. The data has been read and stored in a data structure. Add code that will implement the algorithm you identified earlier. Break down the algorithm into smaller parts, implement each part and move ahead. For example, in this Square Pastures problem, you would first find the smallest and biggest x coordinates, and then the smallest and biggest y coordinates. After that, you only need to find which is bigger:  abs(maxY – minY)      abs(maxX – minX)

Finally, output the area of the square.

Initially, you may find the implementation part very challenging. It is quite normal to spend 3-4 or more hours on a bronze level USACO problem. As you work on more problems, the implementation part starts to come easier, you become better at catching bugs in your program and you start to use techniques that you remember from previous problems.

Test the program
Test cases are provided along with each contest problem. Run the program and observe the output if it fails for any test cases. You could also add a few prints in your program to narrow down the lines of code that need modification. Furthermore, use logic to make changes in your program — make changes in the program with a purpose, not just using a trial and error method.

What next?
Try to complete the Square Pastures problem in the USACO portal. Then, try some more bronze level problems. Remember, it is perfectly OK to spend many hours and even days on one problem. The satisfaction of finally solving it will be worth it. After solving a few bronze level problems independently, you could consider registering for the next USACO competition. It is free and fun, and you score points even if a few test cases pass.